3.8 – Module Summary

In this module, we have covered:

  • Density and specific gravity
  • Dimensional Homogeneity
  • Process and Instrumentation Diagram (P&ID)
  • Equilibrium (Solid-Liquid, Solid-Vapour and Liquid-Liquid)
  • Temperature systems ( Kelvin, Celsius, Fahrenheit, Rankine )
  • Recycle and purge
  • Separator
  • Splitter

The purpose of this notebook is to give a summary of all the topics covered, and to give additional practice problems for topics focused more heavily in CHBE 241, which are bolded in the list above. The practice qustions will try and include most topics covered in the module.

3.8.0 – Density and specific gravity

Density is the amount of mass per unit volume, and specific gravity (S.G.) is the ratio of density of the object to the density of a standard, usually water for a liquid or solid, and air for a gas. Density of a mixture can be estimated using mass fractions of mixture components and the components’ densities.

\[Density = \rho\]
\[Specific \space gravity = \frac{{\rho}_{sample}}{{\rho}_{H_2O}}\]
\[\overline\rho = \sum_{i=1}^{n} {x_i}{\rho}_i\]

3.8.1 – Dimensional homogeneity

Dimensional homogeneity is the concept where the dimensions of variables on both sides of an equation are the same. If the units are the same, it follows that the dimensions of each term must be the same.

\[Length = (Length/Time) \times (Time)\]

An equation could be dimensionally homogenous but invalid if the equation is also not fully-balanced i.e.

\[2M = M\]

is only valid for 1 case of M.

3.8.2 – Temperature systems ( Kelvin, Celsius, Fahrenheit, Rankine )

Conversion table (Kelvin based)

  From kelvins To kelvins
Celcius [°C] = [K] − 273.15 [K] = [°C] + 273.15
Fahrenheit [°F] = [K] ×  \(9⁄5\) − 459.67 [K] = ([°F] + 459.67) ×  \(5⁄9\)
Rankine [°R] = [K] ×  \(9⁄5\) [K] = [°R] ×  \(5⁄9\)

Conversion table (Celsius based)

  From Celsius To Celsius
Kelvin [K] = [°C] + 273.15 [°C] = [K] - 273.15
Fahrenheit [°F] = [°C] ×  \(9⁄5\) + 32 [°C] = ([°F] - 32) ×  \(5⁄9\)
Rankine [°R] = [°C** + 273.15**] ×  \(9⁄5\) [°C] = [°R] ×  \(5⁄9\) - 273.15

3.8.3 – Practice questions

The following practice problems aim to take the 3 mass balance scenarios (Splitter, Recycle & Purge and Separator streams) and explore all 3 in a single process.

Practice 1

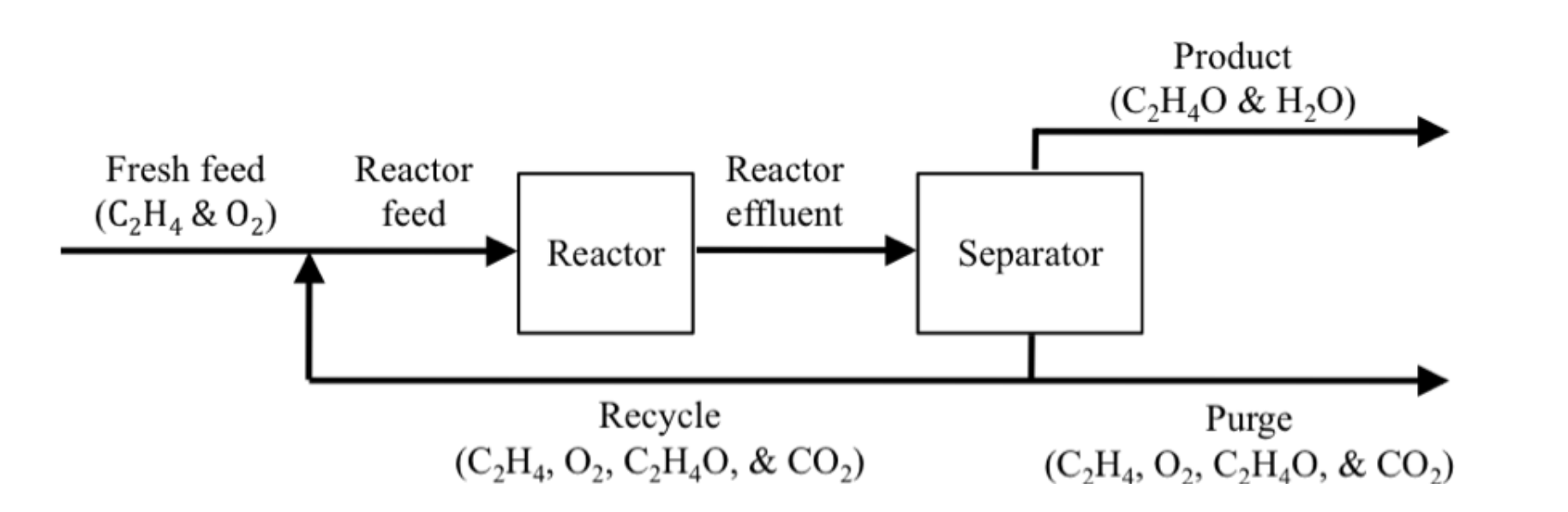
Figure 1.

Figure 1.

A fresh feed of 50% ethylene ( \(C_2H_4\) ) is fed into a process that produces acetaldehyde( \(C_2H_4O\) ) and water as products. To increase the efficiency of the the system, a recycle stream from the separator bottom feed is fed back into the reactor feed. A purge stream carries 15.5 kg \(C_2 H_4/hr\), 15.4 kg \(O_2/hr\), 1.1 kg \(C_2 H_4 O/hr\) and 18 kg \(CO_2/hr\) out of the process. Given that the separator bottom feed flow rate is \(150 \space kg/hr\) and its constituents are 50% \(C_2 H_4\), 20% \(O_2\), 20% \(C_2 H_4 O\) and 10% \(CO_2\). What are the constituents of the:

  1. recycle stream
  2. fresh feed
  3. reactor feed? Give the answer in mass flow rates of each constituent.